중심극한정리가 무엇인지 알아보기 전에 알아야 할 개념이 있다.
1. 중심극한정리 사전 배경지식
- 모집단 분포, 표본 분포, 표집 분포
이 세가지 분포에 대해 개념을 알아야 한다.
(1) 모집단 분포
- 따로 설명할 필요없이 연구할 대상이 되는 모집단이 이루는 분포이다.
(2) 표본 분포
- 모집단에서 N가지 랜덤하게 샘플링했을 때 그 표본이 나타내는 분포를 의미한다.
예를 들어 성인 남성의 키를 조사하고자 100명을 랜덤하게 추출했을 때
171cm, 180cm, 179cm .... 와 같이 표본 X가 그리는 분포이다.
(3) 표집 분포
- 모집단 분포와 표본 분포는 실재하는 분포이다. 즉 모집단 분포의 경우 시간과 돈(?)이 많으면
알아낼 수도 있으며 표본 분포 또한 당연히 직접 샘플링했으므로 실제 존재하는 분포이다.
그런데 표집분포는 실재하는 분포가 아닌 가상의 분포이자 이론적으로 존재하는 분포이다.
바로 표본 분포를 무한히 반복했을 때, 표본의 평균이 그리는 분포가 바로 표집분포이다.
예를 들어 성인남성 100명을 랜덤하게 추출했을 때 첫 100명을 뽑아 평균 낸 값이 M1이라 하고
그 다음 100명을 뽑아 평균 낸 값을 M2라 하고 .. 이와 같이 무한히 추출하여 M1 ~ Mn 까지 얻었을 때
이 값들이 그리는 분포가 바로 표집분포이다.
표집분포는 표본을 무한히 반복해서 얻어냈다고 가정하기에 실제로 얻어내는 것은 불가능하며
이론적 분포라 하는 것이다.
중심극한정리는 이 표집분포에 관한 내용이다.
2. 중심극한정리의 정의
먼저 중심극한정리의 정의부터 알아보자.
중심극한정리의 정의는 크게 3가지로 구성되어 있다.
(1) 표집분포의 평균은 모집단의 평균과 같고
(2) 표준편차(오차)는 모집단의 표준편차를 표본 크기의 제곱근으로 나눈 값과 같으며
(3) 표집분포는 정규분포를 그리게 된다.
하나씩 곱씹어 보자.
첫 번째. 표집분포의 평균은 모집단의 평균과 같다.
무한히 뽑은 표본 M1~Mn 의 평균은 왠지 모집단의 평균과 맞을 것 같다. 이건 나름대로 직감적이다.
(물론 중심극한정리가 감에 의한 것은 아니고 엄연히 수학적 증명에 의한 것이지만
최대한 수식은 배제하고자 함)
두 번째. 표준편차(오차)는 모집단의 표준편차를 표본 크기의 제곱근으로 나눈 값과 같다.
예를 들어 대한민국 성인 남성의 키의 평균은 173cm고 표준편차는 5cm라고 하자.
내가 다니는 직장 내 남자 사원들의 키가 평균에 부합하는지 확인하기 위해
랜덤하게 25명을 뽑았다고 하자.
나는 랜덤하게 25명 한번만을 선출하였지만 만약 추출을 무한히 반복한다면 중심극한정리에 의해
추출 결과는 평균이 173cm, 추출한 값들간의 표준편차(오차)는 5cm / sqrt(25) = 1cm 가 된다는 뜻이다.

표집분포의 표준편차는 1cm가 되는데,
참고로 표집분포의 표준편차는 표준편차라 부르지 않고 표준오차(Standard Error)라 부른다.
모집단의 표준편차는 5cm인 반면 표집분포의 표준오차는 1cm 임을 눈여겨 봐야 한다.
만약 25명씩 추출하는 것이 아니라 100명을 추출한다면 어떻게 될까?
중심극한정리에 의해 표집분포의 표준오차는 5cm / sqrt(100) = 0.5 cm가 된다.

결국 랜덤추출을 몇 명씩 하냐에 따라 표본들이 그리는 분포는 달라지게 되며
직관적으로 생각했을 때 표본의 크기 N이 커질수록, 예를 들어 만명 또는 십만명씩 추출한다면
샘플링간의 차이는 줄어들 것이라 생각해볼 수 있다.
그렇기에 샘플링 분포가 그리는 그래프는 좁아지게 될 수밖에 없다.
일반적으로 N=20 혹은 30 이상이면 중심극한정리를 충족한다고 한다.
세 번째, 표집분포는 정규분포를 그린다.
모집단의 분포가 어떻든간에 표집분포는 정규분포를 그리게 된다는 뜻이다.
예를들어 주사위의 분포는 각 값이 1/6을 가지는 균일분포라 하더라도
주사위를 N회 던져 얻은 평균값들을 얻고, 이 행위를 무한히 반복했을 때
평균의 평균은 중심극한정리에 의해 정규분포를 그리게 된다는 뜻이다.
이 정도면 중심극한정리가 무엇인지는 알 수 있을듯 하다.
그런데 중심극한정리가 왜 중요한가?
3. 중심극한정리의 역할
중심극한정리는 표본을 이용한 가설검정을 하는데 이용된다.
위에서 예를 들었던 대한민국 남성의 키는 173cm에 표준편차는 5cm 에서 예시를 이어가보자.
내가 다니는 직장에서 랜덤하게 25명을 뽑았더니 평균 175cm로 조사되었다.
직장내 남성들의 키가 대한민국 남성의 키보다 크다고 볼 수 있을지 판단 내릴 수 있을까?
이 판단을 하는데 중심극한정리가 이용되는 것이다.
즉 표본을 가지고 무언가 통계적 판단을 할 때 중심극한정리가 필요하다고 이해하면 된다.
대부분의 통계적 판단은 표본을 가지고 하므로 중심극한정리없이는 많은 가설검정이 불가능하다고 이해하면 된다.
이 정도면 중심극한정리가 얼마나 중요한지 감이 왔으리라 생각된다.
그럼 예시를 이어서 직장내 남성이 대한민국 남성보다 키가 클까?
이를 판단하기 위해 유의수준을 .05로 설정하고 귀무가설과 대립가설을 설정해보자.
귀무가설: 직장내 남성키 <= 173cm
대립가설: 직장내 남성키 > 173cm
직장내 남성의 키가 173cm보다 큰지를 검정하기 때문에 일방적 검정 or 단측검정을 수행하게 된다.
귀무가설이 옳다는 가정하에 표본 추출을 무한히 반복한다면 중심극한정리에 의해 위에서 봤던 분포가 그려지게 된다.
내가 얻은 표본은 이 표집분포 위에 놓여지게 되며 여기서 채택역과 기각역이 설정된다.
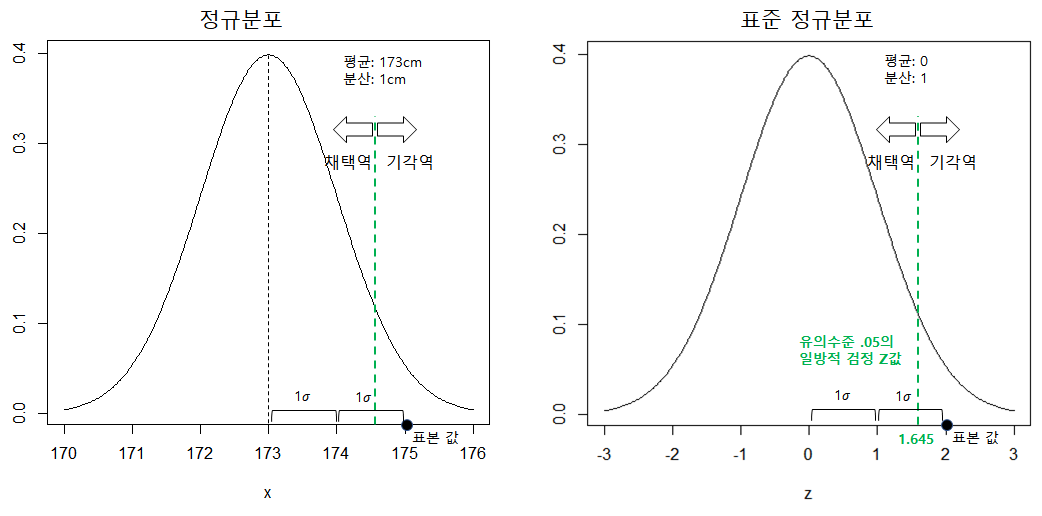
왼쪽은 정규분포이고 오른쪽은 표준 정규분포로 변환시킨 결과인데 어떤 그래프를 봐도 상관없다.
참고로 일방적 검정에서 유의수준 .05의 Z값은 +1.645인데 1.645 표준편차를 의미한다.
왼쪽 그래프에서 1표준오차는 1cm이므로 표본이 173 +1.645 cm 보다 크면 기각한다는 것을 의미한다.
일반적으로는 표준 정규분포를 사용하므로 표준 정규분포를 도입한다면
평균이 0이고 표본 값 Z는 (X변량 - 평균) / 분산 공식에 의해
(175cm - 173cm) / 1cm = 2가 된다.
여기서 분산을 계산할 때는 표집분포의 표준오차를 사용한다.
따라서 표본의 Z값 2 > 1.645 이므로 유의수준 .05 수준에서 귀무가설을 기각하며 직장 내 남성들의 키는 대한민국 남성 키의 평균인 173cm보다 크다고 할 수 있다.
요약하자면 표본에 대해 검정을 수행할 때 기각역과 채택역은
모집단 분포에 대해 설정하는 것이 아니라 중심극한정리 기반의 표집 분포 위에 설정한다.
그렇기에 중심극한정리는 표본을 통해 검정을 수행할 때 반드시 필요한 기초이론이 된다.
위에서 예시를 Z검정도 그렇고 이후에 배울 t검정도 그렇고 모두 중심극한정리를 바탕으로 하고 있다.
댓글